Cordell Green is known for his logicist approach to planning, in which desired situations are expressed as logical formulae in the situation calculus, and a resolution-based prover discovers a proof for the existence of a plan eventuating in satisfying such a situation. Mainstream AI has gradually left this method behind because of its supposed intractibility, but new research shows that Green’s Method (GM) for planning can be used in a surprisingly efficient manner with help from some forms of automated natural deduction.
John Pollock’s OSCAR is a cognitive agent driven by a nonmonotonic defeasible reasoner which showed great promise up until Pollock’s premature death, which left OSCAR short of a fully mature state. Fortunately, recent research in the RAIR (Rensselaer Artificial Intelligence and Reasoning) Lab by Kevin O’Neill has restored much of OSCAR to its former glory, and OSCAR can once again be run as a natural-deduction prover from the RAIR-Lab website. And even though OSCAR’s built-in planning system remains under reconstruction, OSCAR can still plan surprisingly well using GM in unsorted first-order logic.
By using a direct analogue of GM within OSCAR, this method becomes a truly viable utility for logic-based planning. The reason derives comes from OSCAR’s method of epistemic reasoning: OSCAR uses an interest-driven approach to natural deduction, which in turn uses backwards reasoning to simplify complex goal constraints into more manageable partial plans. Whereas a resolution-based prover must reason using an answer literal containing a partial plan and compare this with any given goal constraint, OSCAR can repeatedly instantiate these partial plans directly into the goal until it has met a directly reachable situation that satisfies the goal.
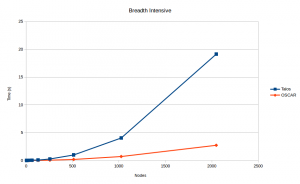
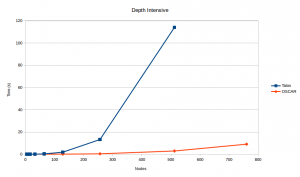
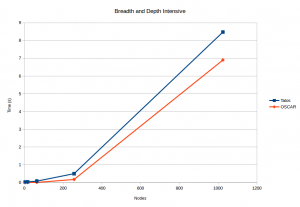
Below are a series of graphs depicting performance of both OSCAR, a natural-deduction prover, and Talos, RAIR Lab’s SPASS-based resolution prover, over a series of problems of varying size. For any given problem, the axiom set defines a directed acyclic graph (dag) with one source node and b disjoint branches of depth d. The depth-intensive dags have a breadth of 2 and a depth of n2; the breath-intensive dags have a depth of 2 with n2 branches, and the breadth-and-depth-intensive dags have equal breadth and depth. OSCAR performs substantially faster on both the depth-intensive and breadth-intensive problems. However, as can be seen, the difficulty of depth-and-breadth-intensive problems begins to limit OSCAR’s performance. At any rate, OSCAR performs not only on par, but on average significantly faster, than Talos. Clearly, natural deduction-based reasoning is a strong contender with resolution when applied to GM for planning.
It turns out that this tactic isn’t completely unique. Pollock’s version of OSCAR initially came with its own planning system, which created plans by sending plan queries to OSCAR’s epistemic reasoner (a process which Pollock dubbed doxastification). GM operates on the same principle: use a proof technique (in GM’s case, resolution) in order to discover suitable plans. The two ideas are not completely isomorphic; doxastification is merely the first process in OSCAR’s extensive planning system meant to simulate a so-called artilect (essentially, an artificial intellect, bereft of emotions and a body), while GM is simply a proof-theoretic method for planning; but it is useful to note the analogy between the two.
Possibly the most beneficial aspect of using GM via natural deduction is not only its speed, but also its ability to provide a machine-generated (though human-readable) proof for any given plan. This allows the agent to contribute relevant and usable logic-based reasons for its plans, aiding in planning processes beyond discovery, such as plan evaluation, modification, and adoption.