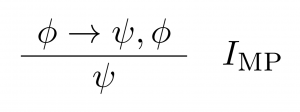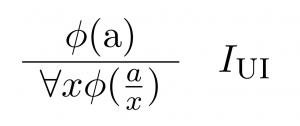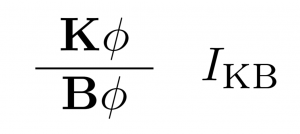What is a cognitive calculus C, and why is it denoted with the two words in question? (We use ‘C‘ here as an arbitrary variable ranging over (the uncountably infinite space of) all cognitive calculi). In keeping with the mathematical-logic literature, we first note that a logical system L is a triple < L, I, S > where L is a (often) typed formal language (based therefore on an alphabet and a formal grammar determinative of well-formed formulae), I is a set of inference schemata, and S is a formal semantics of some sort. For example, the familiar propositional calculus comprises a family of simple logical systems; the same holds for first-order logic; both families are of course at the heart of AI. In the case of both of these families, a frequently included particular inference schema is modus ponens, that is
And in the case of the latter family, often universal introduction is included in a given I; a specification of this inference schema immediately follows.
Note that both the propositional calculus and first order logic are extensional, which means essentially that the meaning of any formula \phi in the relevant languages are given by compositional functions operating solely on the internal components of \phi. If we for example know that \phi is false, then we know that the meaning of \phi \rightarrow \psi is true, for any \psi in the language, for both of these logical systems.
Moving from the concept of a logical system to that of a cognitive calculus is straightforward, and can be viewed as taking but three steps, to wit:
S1: Expand the language of a logical system to include
- modal operators that represent one or more mental
verbs at the human level standardly covered in human-level cognitive psychology (e.g. see any standard, comprehensive textbook on human-level cognitive psychology), and regarded to be so-called “propositional attitudes” that give rise to propositional-attitude-reporting sentences, where these sentences are represented by operator-infused formulae in a cognitive calculus. Such verbs include: knowing, believing, deciding, perceiving, communicating, desiring, and so on. Note that such verbs break the bounds of extensionality, and hence make any logic that captures them an intensional logic. This step is the reason why we speak of a cognitive calculus. - meta-logical expressions (such as that from a set \Phi of formulae a particular formula \phi can be proved). This step is a necessary, preparatory step for S2.
S2: Delete S; if desired, move selected elements of S into I, which requires casting these elements as inference schemata that employ meta-logical expressions secured by prior step S1.2. S2 reflects the fact that cognitive calculi have purely inferential semantics, and hence are aligned with the tradition of proof-theoretic semantics. (In particular, cognitive calculi thus do not employ possible-worlds semantics for modal operators.) We might for instance wish to include an inference schema that regiments the idea that an agent knows that which is provable from what she knows. Step S2 is the reason why we speak of a cognitive calculus (instead of e.g. a cognitive logic, or cognitive logical system).
S3: Expand I as needed to include inference schemata that involve the operators from S1.1. For instance, where K is the modal operator for ‘knows’ and B for ‘believes’, we might wish to have this inference schema in a given C: